Consider the following discrete probability distribution. – Consider the following discrete probability distribution: a fundamental concept in probability theory that underpins various real-world applications. This guide delves into the intricacies of discrete probability distributions, exploring their properties, functions, and practical significance.
Discrete probability distributions provide a framework for modeling random variables that can take on a finite or countably infinite number of distinct values. Understanding these distributions is crucial for analyzing phenomena involving uncertainty and making informed decisions in diverse fields.
Discrete Probability Distribution
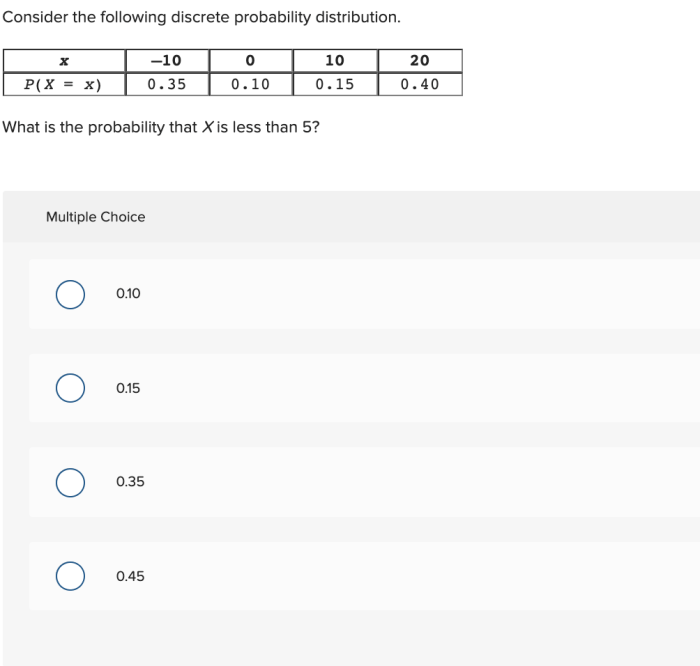
A discrete probability distribution assigns probabilities to each possible outcome of a random variable that can take on a finite or countable number of distinct values.
For example, the number of heads that appear when a fair coin is flipped is a discrete random variable that can take on the values 0 or 1. The probability of getting 0 heads is 1/2, and the probability of getting 1 head is also 1/2.
Properties of a Discrete Probability Distribution, Consider the following discrete probability distribution.
- The sum of the probabilities of all possible outcomes is equal to 1.
- The probability of any one outcome is between 0 and 1.
Probability Mass Function
The probability mass function (PMF) of a discrete random variable is a function that gives the probability of each possible outcome.
To calculate the PMF, we divide the probability of each outcome by the total number of possible outcomes.
For example, the PMF of the number of heads that appear when a fair coin is flipped is:
“`P(X = 0) = 1/2P(X = 1) = 1/2“`
Cumulative Distribution Function
The cumulative distribution function (CDF) of a discrete random variable is a function that gives the probability that the random variable takes on a value less than or equal to a given value.
To calculate the CDF, we add up the probabilities of all the outcomes that are less than or equal to the given value.
For example, the CDF of the number of heads that appear when a fair coin is flipped is:
“`F(X = 0) = P(X = 0) = 1/2F(X = 1) = P(X = 0) + P(X = 1) = 1“`
Expected Value
The expected value of a discrete random variable is the average value of the random variable.
To calculate the expected value, we multiply each possible outcome by its probability and then add up the results.
For example, the expected value of the number of heads that appear when a fair coin is flipped is:
“`E(X) = 0
- P(X = 0) + 1
- P(X = 1) = 1/2
“`
Variance: Consider The Following Discrete Probability Distribution.

The variance of a discrete random variable is a measure of how spread out the random variable is.
To calculate the variance, we first calculate the expected value of the random variable. Then, we square the difference between each possible outcome and the expected value, multiply the result by the probability of that outcome, and add up the results.
For example, the variance of the number of heads that appear when a fair coin is flipped is:
“`Var(X) = (0
- 1/2)^2
- P(X = 0) + (1
- 1/2)^2
- P(X = 1) = 1/4
“`
Standard Deviation
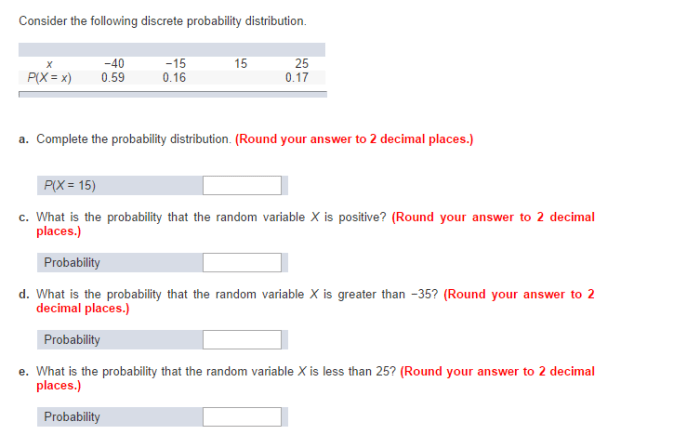
The standard deviation of a discrete random variable is the square root of the variance.
For example, the standard deviation of the number of heads that appear when a fair coin is flipped is:
“`SD(X) = sqrt(Var(X)) = sqrt(1/4) = 1/2“`
Applications of Discrete Probability Distributions
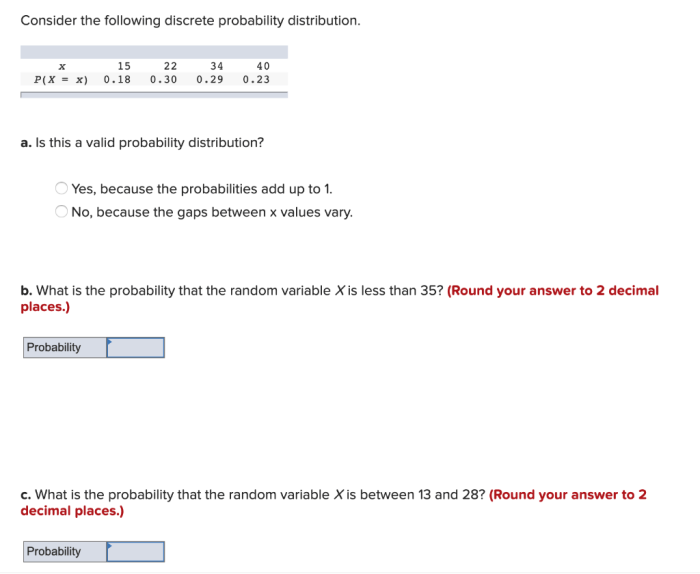
Discrete probability distributions are used in a wide variety of applications, including:
- Gambling: Discrete probability distributions are used to calculate the odds of winning a game.
- Insurance: Discrete probability distributions are used to calculate the probability of an event occurring, such as a car accident or a house fire.
- Marketing: Discrete probability distributions are used to predict the number of customers who will respond to a marketing campaign.
- Quality control: Discrete probability distributions are used to determine the probability of a product being defective.
Query Resolution
What is a discrete probability distribution?
A discrete probability distribution is a function that assigns probabilities to each possible outcome of a random variable that can take on a finite or countably infinite number of distinct values.
How do you calculate the probability mass function of a discrete probability distribution?
The probability mass function (PMF) of a discrete probability distribution is defined as the probability of each possible outcome. It is calculated by dividing the probability of an outcome by the sum of probabilities over all possible outcomes.
What is the cumulative distribution function of a discrete probability distribution?
The cumulative distribution function (CDF) of a discrete probability distribution is defined as the sum of probabilities from the minimum possible outcome up to and including a given outcome. It represents the probability of an outcome being less than or equal to a specific value.